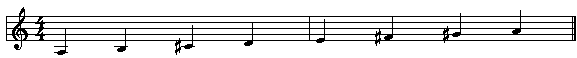|
Costruzione della Scala Minore.
Tutte le scale nascono
da una sequenza ben precisa di toni e semitoni. Riducendo il concetto alla
semplicità, possiamo dire che basta conoscere una sequenza di un certo
tipo o modo di scala per poterne avere la costruzione logica in tutte le
tonalità. Ovviamente, sul lato pratico, la cosa diventa più complicata,
in quanto i tipi di scale (e i relativi modi) sono molti, e di conseguenza
anche la memorizzazione e l'utilizzo musicale ne risulta più complesso.
Abbiamo già analizzato la costruzione di una Scala Diatonica Maggiore, e
abbiamo appreso che seguendo un sistema di logica costruttiva possiamo
costruire da una nota la sua SDM, e questo per tutte le tonalità.
Ricordiamo la sequenza di toni e semitoni di una SDM:
| I° |
II° |
III° |
IV° |
V° |
VI° |
VII° |
VIII° |
In una Scala Minore la sequenza dei semitoni viene a cambiare in quanto la successione degli
intervalli è diversa a seconda del tipo di scala minore che dobbiamo
costruire. Sono tre i tipi di scala minore che dobbiamo analizzare, che
possiamo vedere abbinati alla loro sequenza intervallare.
| I° |
II° |
III°b |
IV° |
V° |
VI°b |
VII°b |
VIII° |
| I° |
II° |
III°b |
IV° |
V° |
VI°b |
VII° |
VIII° |
| I° |
II° |
III°b |
IV° |
V° |
VI° |
VII° |
VIII° |
Il primo modello che
analizziamo è la Scala Minore Naturale, che per comodità abbreviamo
in smn. Come per ogni modello di scala, è conveniente comparare la
successione dei toni e semitoni con la scala maggiore della nota stessa.
La SDM di DO, come ben sappiamo, è costruita in questo modo:

A questo punto, osservando la sequenza intervallare della smn vista sopra,
applichiamo le variazioni sui gradi interessati, e cioè il III°, il VI° e
il VII°. Questi verranno abbassati di 1st: infatti il simbolo bemolle che
potete vedere nello specchietto si riferisce al fatto che viene tolto 1st
dalla nota (grado). In pratica il III° (nota MI) viene abbassato a MIb, il
VI° da LA scende a LAb e il VII° passa da SI a SIb. Ecco quindi la Scala
Minore Naturale di DO:

Proviamo ora a costruire una nuova scala minore, ad esempio in tonalità di
LA. Vediamo prima la Scala Diatonica Maggiore di LA.
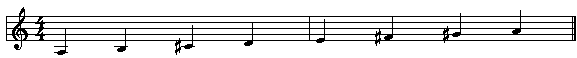
Ora, per costruire la smn di LA, abbassiamo di 1st il III° (da DO# a DO),
il VI° (da FA# a FA) e il VII° (da SOL# a SOL). Questa è la scala:

Potete vedere le scale minori naturali in tutte le tonalità,
ma provate anche a costruirle utilizzando la tecnica di cui sopra.
Ora possiamo anche precisare una caratteristica che lega una SDM ad una smn.
Una SDM ha una sua relativa minore che nasce sul VI° della SDM stessa.
Ad esempio: sul VI° della SDM di DO troviamo la nota LA. Facendo partire la
successione delle note appunto dalla nota LA, e seguendo le note della scala
di DO, otteniamo una sequenza di note che, analizzandola, è la stessa della
scala minore naturale di LA. Nell'esempio seguente vediamo la SDM di DO nella prima battuta
e la sua relativa minore, cioè la smn di LA nella seconda battuta.

Da qui la regola che ci indica che una smn può essere definita anche
relativa minore. Quindi, per fare qualche esempio, la SDM di SOL ha la sua
relativa minore nella smn di MI, oppure la SDM di RE ha la sua relativa
minore di nella smn di SI.
La regola può essere anche invertita. Una smn ha la sua relativa
maggiore che nasce sul III° della smn stessa. Quindi, se prendiamo ad
esempio la smn di DO, la sua relativa maggiore la troviamo sul III°, e
cioè sulla nota MIb (ed infatti, sulla scala di MIb maggiore troviamo nel
VI° la nota DO, che ne sarà la sua relativa minore).
Nell'esempio vediamo la SDM di MIb e la sua relativa minore, DOm

|